O delta foi inserido na fórmula de bháskara para as resoluções das equações de segundo grau. Ele está inserido nas equações de 2º grau para que ela possa ter duas raízes – que é o fator principal dessa equação.
Observe sempre que a diferença da equação de 1º grau para a de 2º grau, é apenas o coeficiente x elevado a 2.
A fórmula de bháskara foi definida para estudar as equações de 2º grau, antes do delta ser inserido era a forma mais certa de se calcular esse tipo de conta, seu primeiro modo de resolução era feito por essa fórmula criado por Bháskara Akaria:
Logo que:
x = coeficiente
a, b e c = são os coeficientes dos termos da função
Exercício 1:
Dados
x = ?
a = 5
b = 12
c = 4
Aplicado a fórmula:
Já com a inserção do delta, a maneira mais certa, mais usada e mais indicada e que é usada até hoje para calcular uma equação do 2° grau é:

Sendo:
x = coeficiente
a, b e c = coeficientes dos termos da função
± = uma resolução positiva e outra negativa para diferenciar uma raiz da outra
Δ = radicando ou discriminante
Exercício 2:
Dados
x = ?
a = 1
b = 2
c = -24
Aplicando a fórmula:

As raízes são divididas e observadas em:
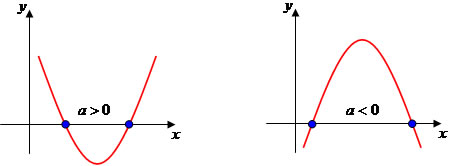
Δ > que 0: são duas raízes reais – são dois pontos que tocam o eixo x.
Δ = 0: são duas raízes reais ou idênticas – só irá tocar o eixo x, sem atravessá-lo.
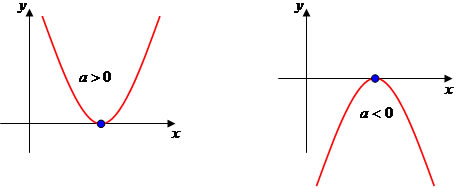
Δ < 0: são duas raízes distintas e não reais – não pode cortar o eixo x, somente o y.
