A Trigonometria é uma área da matemática que estuda as razões dos lados de um triângulo retângulo, aqueles onde um dos ângulos possui a medida de 90º, esse campo também avança em outras direções dentro dessa ciência. A maioria dos estudiosos confabulam e concordam que o cerne desses estudos possa ter partidos de implicações e imbricações da vida prática, por exemplo a necessidade de analisar os relógios do sol. Os estudos trigonométrico partem de três proporções fundamentais, Seno, Cosseno e Tangente.
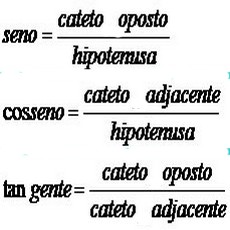
* Seno: é dado pela relação da medida comprimento cateto oposto com a medida do comprimento da hipotenusa.
* Cosseno: é dado pela relação da medida comprimento do cateto adjacente com a medida do comprimento da hipotenusa.
* Tangente: é dado pela relação da medida do comprimento cateto oposto com a medida do comprimento do cateto adjacente.
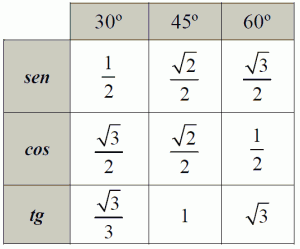
Dentro da Trigonometria exite uma série de ângulos possíveis dentre os quais merecem destaque os ângulos notáveis, que recebem esse nome por aparecerem com maior evidência no cálculos, são eles 30º, 45º e 60º. Suas razões trigonométricas podem ser organizados na seguinte conjectura:

Para cacular seno ou cosseno do primeiro quadrante com ângulos que não estão na figura basta subtrair o valor do ângulo por 180, e importante salientar que nesses casos cosseno sempre terá valor negativo, exemplo:
cos 120 º = 180 -120 = 60= – cos 60º = 1/2
Para o terceiro quadrante cosseno e seno é diminuí 180º e ambos são negativados, no quarto o valor do ângulo é subtraído por 360º, apenas seno surgirá como negativo.
Exercícios :
a) seno 240º=
b) cos 30º=
c) seno 330º=
d) cos 150º=
e) cos 330º=
f) seno 210º=
Respostas: a)- √3/2, b) √3/2,c) -1/2, d) – √3/2, e) √2/2 e f) -1/2