Os números primos são ditos números naturais que só possuem dois divisores, sendo eles o número 1 e ele mesmo. A sua descoberta foi muito importante para a matemática porque eles intitulam o principio teórico de todos os números, tendo mais consistência no Teorema Fundamental de Aritmética.
Esse teorema afirma que todo número inteiro natural, maior que 1, pode ser descrito pelos números primos. Mas destaca que o 1 não pode ser um número primo, pois ele tem apenas um divisor e não pode ser descrito de tal forma.
Através da fatoração, que é a decomposição dos números pelos fatores primos, é possível representar os números de acordo com o teorema.
Exemplos:
* 12: 2x2x3
* 25: 5×5
* 27: 3x3x3
* 40: 2x2x2x5
Eratóstenes (285-194 a. C) foi o grande criador dos sistema simples dos números primos, chamado ainda de crivo de Eratóstenes.
Como utilizar o crivo?
1° Visualize o número 2 na tabela;
2° Marque todos os múltiplos dele;
3° Localize o número primo seguinte e visualize seus múltiplos;
4° Repita esse processo até o último número;
5° Todos que forem divisíveis apenas por ele mesmo e pelo número 1 é dito como um número primo.
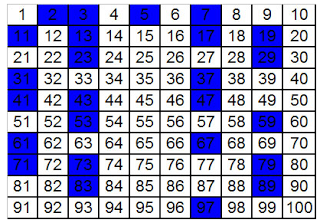
* Números primos destacados em azul.

