Tag: tangente

Publicado em

Identidades trigonométricas fundamentais

Identidades trigonométricas fundamentais

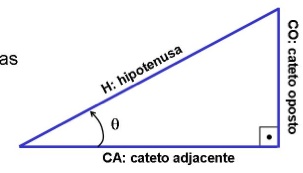
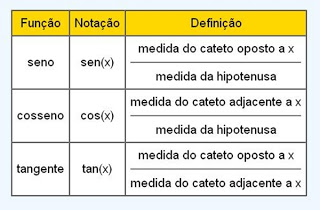
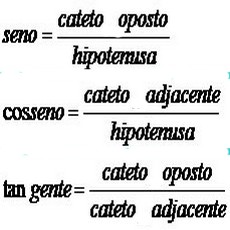
A identidade trigonométrica fundamental é responsável por expressar o teorema de Pitágoras de maneira trigonométrica. Para realizar esse procedimento, é necessário que seja utilizado uma fórmula que contenha a soma dos ângulos, que é a relação primordial das funções entre o cosseno e o seno.

Observação: Somente depois que ambas funções são definidas que as outras podem ser derivadas.

Funções trigonométricas pertencentes ao mesmo arco

A relação descrita abaixo se trata da função fundamental da identidade trigonométrica:

sen²x+cos²x=1

tg x=sen x/cos x

cot g x=cos x/sen x

sec x=1/cos x

cos sec x=1/sen x

» Existem algumas expressões fundamentadas pela relação descrita acima que são muito importantes  para a resolução de funções encontradas em um mesmo arco:

  • » sec² x=tg²x+1;
  • » cos sec² x=cot g²x+1;
  • » cot g x=1/tg x.

Como comprovar a identidade trigonométrica?

Todas as igualdades verificáveis que envolvem as funções trigonométricas são denominadas de identidade trigonométrica. Veja alguns exemplos abaixo:

» Exemplo 1:

tg x * cos x = sen x

sen x/cos x * cos x = sen x

sen x = sen x

» Exemplo 2:

(1 – cos² x) * (cot g² x+1) = 1

(1 – cos² x) * (cos² x/ sen² x + 1) = 1

(1 – cos² x) * (cos² x + sen² x/sen² x) = 1

sen² x * 1/sen² x = 1

1 = 1

Dicas

Principais identidades trigonométricas:

» tg x = sen x/cos x;

» cot g x = cos x/sen x;

» sec x = 1/cos x;

» cos sec x = 1/sen x;

» sen² x + cos ² x = 1.

Publicado em

Seno, Cosseno, ângulos e tangente resumo e exercícios

A trigonometria e uma das áreas mais importantes da matemática, diversas inovações tecnológicas só foram possíveis graças a esse conhecimento. Constantemente esse assunto aparece em vestibulares e provas de concursos, conheça mais sobre este assunto.

Conhecendo os lados de um triangulo.

catetos

A hipotenusa será sempre o maior lado de um triangulo, enquanto o cateto oposto estará sempre  do lado oposto ao ângulo do seu triângulo, portanto o cateto adjacente será o menor lado entre o cateto oposto é o ângulo.

Seno, cosseno e tangente

Entendo o angulo como valendo o valor de X vejamos uma tabela das formulas destas funções.

tabela

Essa são as formulas para se obter os valores de seno, cosseno e tangente de um ângulo, mas dentro da matemática constantemente aparecem os valos dos ângulos de 30°, 45° e 60°, esse são chamados de ângulos notáveis.

tabela

Para compreender mais como fazer esses cálculos, tente fazer alguns exercícios abaixo:

1) Em um triangulo retângulo, a sua hipotenusa tem a medida de 10 cm, o cateto adjacente mede 8 cm e o seu catato oposto tem a medida de 6 cm. Calcule o seno ( sen ), cosseno (cos ) e a tangente (tag ) deste triângulo.

2) Um triângulo retângulo  tem a medida de sua hipotenusa igual a 8 cm, sabendo-se que o valor do ângulo desse triângulo é de 30° calculo o valor de seu cateto oposto x.

2) Um triângulo retângulo possui um ângulo que mede 37°, a sua hipotenusa mede 10 cm descubra valor de seu cateto oposto x.

respostas:

1) seno = 0,6 cosseno = 0,8, tangente = 0,75

2) x = 4

3) x = 6,018

Publicado em

Seno cosseno e tangente de 30 45 e 60: Explicação e Exercícios

A Trigonometria é uma área  da matemática que estuda as razões dos lados de um triângulo retângulo, aqueles onde um dos ângulos possui a medida de 90º, esse campo também avança em outras direções dentro dessa ciência. A maioria dos estudiosos confabulam e concordam que o cerne desses estudos possa ter partidos de implicações e imbricações da vida prática, por exemplo a necessidade de analisar os relógios do sol. Os estudos trigonométrico partem de três proporções fundamentais, Seno, Cosseno e Tangente.

Formula do seno,cosseno

* Seno: é dado pela relação da medida comprimento cateto oposto com a medida do comprimento da hipotenusa.

* Cosseno: é dado pela relação da medida comprimento do cateto adjacente com a medida do comprimento da hipotenusa.

* Tangente: é dado pela relação da medida do comprimento cateto oposto com a medida do comprimento do  cateto adjacente.

Dentro da Trigonometria exite uma série de ângulos possíveis dentre os quais merecem destaque os ângulos notáveis, que recebem esse nome por aparecerem com maior evidência no cálculos, são eles 30º, 45º e 60º. Suas razões  trigonométricas podem ser organizados na seguinte conjectura:

notáveis seno cosseno

Para cacular seno ou cosseno do primeiro quadrante  com ângulos que não estão na figura basta subtrair o valor do ângulo por 180, e importante salientar que nesses casos cosseno sempre terá valor negativo, exemplo:

cos 120 º = 180 -120 = 60= – cos 60º = 1/2

Para o terceiro quadrante cosseno e seno é diminuí 180º e ambos são negativados, no quarto o valor do ângulo é subtraído por 360º, apenas seno surgirá como negativo.

Exercícios :

a) seno 240º=

b) cos 30º=

c) seno 330º=

d) cos 150º=

e) cos 330º=

f) seno 210º=

Respostas: a)- √3/2, b) √3/2,c) -1/2, d) – √3/2, e) √2/2 e f) -1/2