A Geometria é uma área da Matemática que estuda as propriedades e medidas de figuras no plano e no espaço. Ela é essencial para o estudo de diversas áreas, como Física, Engenharia, Arquitetura, entre outras. Neste artigo, vamos abordar alguns exercícios resolvidos e explicados passo a passo para facilitar o entendimento dos conceitos geométricos.
1. Perímetro e área de figuras planas:
Vamos iniciar com um exercício simples de cálculo do perímetro e área de um retângulo. Suponha que temos um retângulo com lados de medidas 5 cm e 8 cm. Para calcular o perímetro, basta somar os comprimentos de todos os lados do retângulo: 2*(5+8) = 26 cm. Já para calcular a área, basta multiplicar a medida da base pela altura: 5*8 = 40 cm².
2. Teorema de Pitágoras:
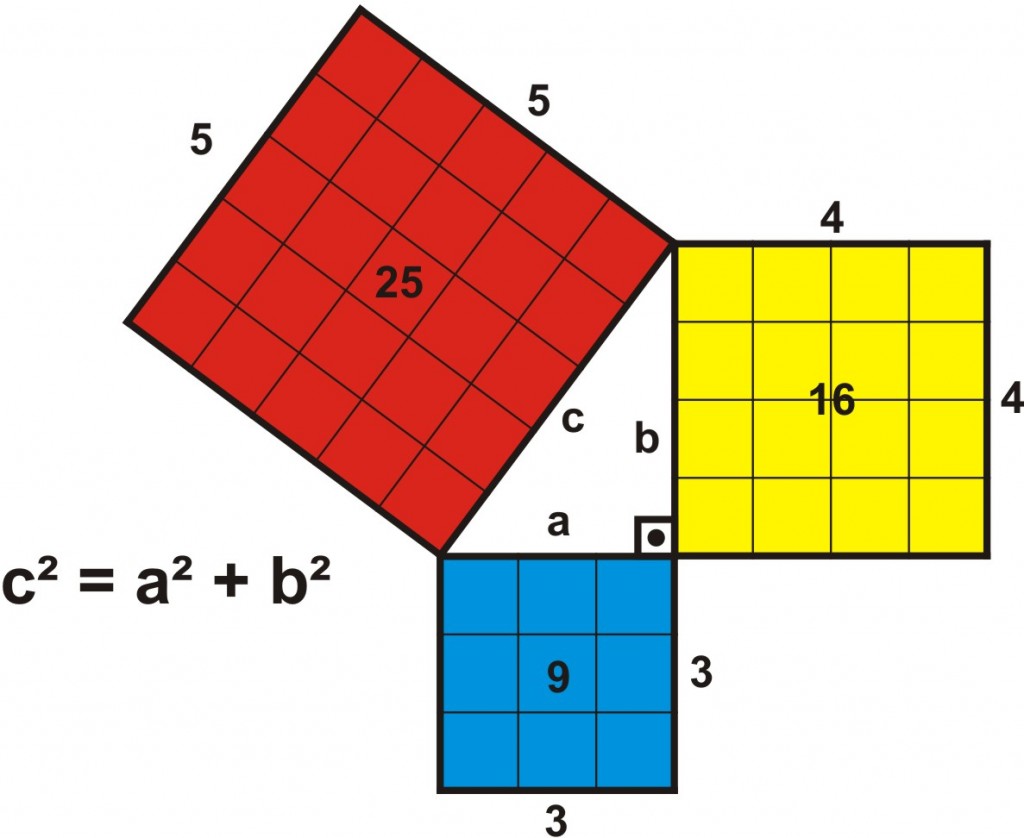
O Teorema de Pitágoras é fundamental na Geometria, e podemos utilizá-lo para resolver diversos tipos de problemas. Vamos resolver um exercício envolvendo um triângulo retângulo. Suponha que temos um triângulo com catetos de medidas 3 cm e 4 cm. Para calcular a medida da hipotenusa, basta aplicar o Teorema de Pitágoras: a² + b² = c², onde a e b são os catetos e c é a hipotenusa. Substituindo os valores, temos: 3² + 4² = c², 9 + 16 = c², c² = 25, c = √25, c = 5 cm.
3. Volume de sólidos geométricos:
Vamos agora resolver um exercício de cálculo do volume de um cilindro. Suponha que temos um cilindro com raio de 4 cm e altura de 6 cm. Para calcular o volume do cilindro, utilizamos a fórmula V = πr²h, onde r é o raio e h é a altura. Substituindo os valores, temos: V = π*4²*6, V = π*16*6, V = 96π cm³.
Esses são apenas alguns exemplos de exercícios resolvidos de Geometria. É importante praticar e entender os conceitos geométricos, pois eles são fundamentais para o desenvolvimento de diversas habilidades matemáticas. Lembre-se de sempre revisar as fórmulas e propriedades geométricas, e praticar com frequência para melhorar o seu desempenho nesta área. Espero que este artigo tenha sido útil para você e que tenha facilitado o seu entendimento dos conceitos geométricos.